Studio Session 6
Electromagnetic waves
In classical physics light is assumed to be an electromagnetic wave.
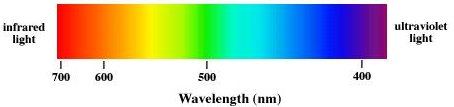
Electromagnetic waves are categorized according to their frequency f or,
equivalently, according to their wavelength λ. The speed of any
electromagnetic waves in free space is the speed of light c = 3*108
m/s. Electromagnetic waves can have any wavelength λ or any frequency f
as long as λf = c. Visible light has a wavelength range from ~400 nm to
~750 nm. Violet light has a wavelength of ~400 nm, and a frequency of
~7.5*1014 Hz. Red light has a wavelength of ~700 nm, and a
frequency of ~4.3*1014 Hz.
Electromagnetic (EM) waves are changing electric and magnetic
fields, carrying energy through space. EM waves require no medium, they
can travel through empty space. Let E denote the electric field
vector and B the magnetic field vector of the EM wave. For
electromagnetic waves E and B are always perpendicular to each
other, and perpendicular to the direction of propagation of the wave.
In general we pay more attention to the electric field
E, because
detectors such as the eye, photographic film, and CCDs interact with the
electric field.
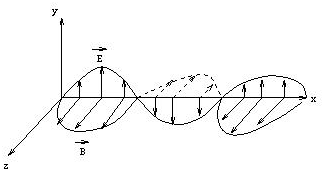
Electromagnetic waves are transverse waves. In this session you will investigate various polarization effects.
Equipment Needed:
- Optical rail with post holders
- Pasco light sensor (CI-6504A)
- Diode laser
- 3 polarizers in rotation stages
- Glass slide
- Screen
Open a Microsoft Word document to keep a log of your experimental procedures,
results and discussions. This log will become your lab report. Address the
points highlighted in blue. Answer all questions.
The inverse square law
All electromagnetic waves transport energy through space.
If a small source, for example the filament in a light bulb,
emits light, the light can be seen from every direction. At a distance
r from the source, the light energy emitted by the source has spread over an
area of 4πr2, the surface area of a sphere with radius r, centered at
the source. Since this area increases with the square of the distance from
the source, the energy flux or intensity I of the electromagnetic light wave,
i.e. the energy per unit area per unit time, decreases proportional to
the inverse square of the distance from the source.
I proportional 1/r2
This inverse square law is a consequence of energy conservation.
The energy of any wave is proportional to the square of its
amplitude, so E2max is proportional 1/r2, or Emax
is proportional 1/r. The amplitude of an electromagnetic wave emitted by a
point source (ideally a single accelerating charge) decreases as 1/r.
Experiment 1:
A small bright light bulb will be your point source of light,
and you will use the Pasco light sensor (CI-6504A) to monitor the intensity as a
function of the distance between the filament and the sensor. The sensor
connects to the Pasco 850 interface and outputs light intensity falling onto its active area
measured in arbitrary units. You will check if
this intensity decreases proportional to the inverse square of the distance
between the sensor and the source.

- The light bulb and the sensor are mounted on the optical rail. The
sensor and the
filament of the light bulb should be at the same height and face each other.
- Plug the sensor into channel B of the Pasco 850 interface.
- Open the Capstone program.
- In the Capstone program, click the Hardware Setup
button, double click Analog Channel B and choose to add a light sensor.
- From Displays, select the Digits icon and choose to
measure Light Intensity (%).
- In the Controls panel select the Fast Monitor Mode and then
click the Monitor icon.
- The light intensity will be displayed. Initially it is proportional to
the amount of background light falling onto the sensor. To keep this
background as low as possible, turn off the room lights.
- Record the background intensity IB
in units of %.

 Turn on the light bulb by rotating the lens counterclockwise and removing it
completely.
Turn on the light bulb by rotating the lens counterclockwise and removing it
completely.- Let dsb be the location of the sensor base
on the optical rail. The initial location should be 20 cm.
- The actual distance, dact, between the filament
tip and the sensor at dsb = 20 cm is 5 cm.
- The offset distance doff = dsb
- dact is 15 cm.
- Download and open this Excel
file. It contains a table with the following headings.
| dsb |
I |
r = dsb - doff |
1/r2 |
I - IB |
- Move the sensor back in 2 cm steps and record the measured
intensity I
for each sensor base position dsb in the table for 10 successive base
positions. When you are done taking data, close the Capstone program.
- Create calculated columns, r = dsb - doff, 1/r2, and
I =
I - IB. I - IB is the measured intensity
I at a
distance r = dsb - doff from the source.
- Produce a plot of I - IB versus 1/r2.
If the intensity decreases proportional to the inverse square of the
distance between the sensor and the source, then this plot should show a
straight line.
- Label the axes of your plot. (Intensity (I) versus 1/distance2
(cm-2)) Paste the plot into your log.
- Discuss your result with your group members
and record the main points of your discussion. Does your plot show a
straight line? If yes, what does this mean? If no, what
could be the reason for this result?
Polarization
Activity 1:
If light propagates through a transparent material such as water or glass, it
interacts in various ways with the atoms or molecules that make up the material.
This interaction can be wavelength and polarization dependent. Due to the
interaction, light moves through a transparent material with an apparent speed v = c/n.
The index of refraction n is a property of the material. It is greater
than 1, so that v is less than c. In most transparent materials the index
of refraction depends slightly on the wavelength of the light, and in some
materials it depends on the polarization.
Linear polarization: An
ideal linear polarizer is a material that passes only light waves for which the electric
field vector is parallel to its transmission axis. If E0 is the incident
field vector and the angle between E0 and the transmission
axis is θ, then the magnitude of transmitted field
vector is E0 cosθ, and its direction is the
direction of the transmission axis. The intensity I of an electromagnetic wave
is proportional to the square of the magnitude of the electric field vector. We
therefore have
Itransmitted = I0 cos2θ.
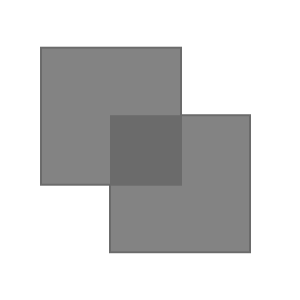 |
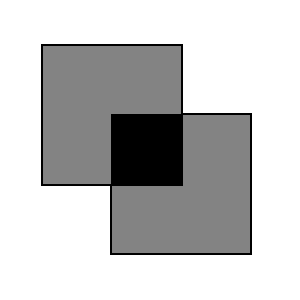 |
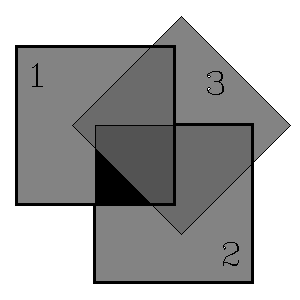 |
Polarizers with parallel
transmission axes |
Polarizers with perpendicular
transmission axes |
Polarizer 3 between
polarizers 1 and 2. |
Spend a few minutes exploring with the three pieces of linear polarizing
material provided to you in an envelope.
Examples:
- Use one polarizing sheet as a polarizer and the other as an analyzer.
Observe the change in transmitted light intensity as either of the sheets is
rotated. Describe and comment on your observations. This combination acts as a "light valve."
- Light reflected from smooth surfaces is polarized. Look through a
single polarizer at the light reflected from a shiny floor, smooth table
top, or sheet of glass. Describe and comment on your observations.
- Light from LCD screens is polarized. Look through a polarizer at
the screen of your laptop or cell phone. Describe and comment on your observations.
Put the pieces of polarizing materials back into the envelope for the next
lab session.
Experiment 2:
In this experiment you will use a linear polarizer to produces a polarized beam and then pass this beam through a second polarizer whose
transmission axis makes an angle θ with respect to the transmission axis of the
first one. You will check that Itransmitted = I0 cos2θ.
This is called the Law of Malus.

Important!
Do not move the bases on the rail. Do not remove the components from
the post holders. Only adjust the height and orientation of the
components.
- Plug the light sensor into channel A of the Pasco 850 interface.
- Open the Capstone program.
- In the Capstone program, click the Hardware Setup button, double click
Analog Channel A and choose to add a light sensor.
- From Displays, select the Digits icon and choose to
measure Light Intensity (%).
- In the Controls panel select the Fast Monitor Mode and then
click the Monitor icon.
- The light intensity will be displayed. Initially it is proportional to
the amount of background light falling onto the sensor. Make sure the
sensor's "Gain" switch is set to 1. To keep this background as low as
possible, turn off the room lights.
- Record the background intensity IB
in units of %.
- The light sensor should be tightened to the optical rail at ~ 80 cm on the rail.
- Your light source for this experiment is a diode laser.
It should be tightened to the optical rail at ~40 cm.
- Two polarizers should be mounted between the laser and the light sensor at ~
60 cm, with their transmission axes aligned vertically. The polarizer
holders should have their dial sides facing away from each other. Make
sure the polarizer disks are perpendicular to the laser beam.
- Adjust the height and angle of the laser, so that the laser beam
falls onto the sensor window. Monitor the light intensity.
(The detector is probably saturated.)
- Loosen the screw on top of the laser
and rotate the laser so that the light intensity changes to ~75% - 85%.
Then tighten the screw again and also tighten the laser post in its
post holder. For the remainder of this experiment leave the
laser and sensor undisturbed.
- After the laser light has passed through the polarizers, it is
~100% polarized along the vertical direction, since the transmission
axis of each polarizer is vertical.
In Excel create a table.
| angle (deg) |
I |
angle (rad) |
I - IB |
I0*cos2(angle) |
- You will now rotate the second polarizer with respect to the first one.
Start by recording the measured intensity for zero degrees, when both
polarizers are aligned.
- Rotate the second polarizer in 10o steps. For angles between 0 and 180o in 10o steps measure
and record the intensity I in the table.
-
When you are done taking data click Stop.
- Create calculated columns
I - IB and I0*cos2(angle), with the angle
in radians. I0 is the intensity you measured when the second polarizer
angle was 0.
- Create a plot of
I - IB and I0*cos2(angle) versus angle (rad).
Label the axes.
- Paste the plot into your log.
- Discuss your result with your group members and
record the main points of your discussion. Have you verified the
Law of Malus? How can you tell? No experiment is perfect, there
are always uncertainties. Are your uncertainties small enough so that
you can tell one way or the other. Make reasonable arguments.
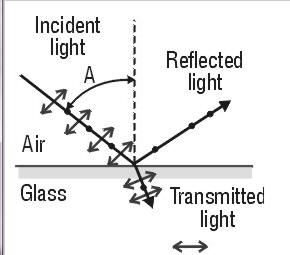 Polarization by reflection
Polarization by reflection
When unpolarized light is incident on a boundary between
two transparent materials, for example on an air-glass boundary, then the
reflected and transmitted components are partially plane polarized. The
reflected wave is 100% linearly polarized when the incident angle is equal to
the Brewster angle θB, where tanθB
= n2/n1. The Brewster angle for reflecting off glass
is between 50o and 60o.
Experiment 3:
You will reflect the light from a diode laser off a glass plate. You will make sure that the
incident angle is close to the Brewster angle and verify that light polarized in
the plane of incidence it will not be reflected at the Brewster angle. The
plane of incidence is a plane perpendicular to the reflecting surface that
contains the incident beam.
If the reflecting surface is horizontal, then the
plane of incidence is vertical. The reflected light at the Brewster angle is horizontally polarized and can be blocked by a polarizer with
a vertical transmission axis. If the reflecting surface is vertical, then
the plane of incidence is horizontal, and horizontally polarized light
will not be reflected at the Brewster angle. Then
the reflected light is vertically polarized at the Brewster angle and can be blocked by a polarizer
with a horizontal transmission axis. You will reflect the laser light off
a vertical glass surface (a microscope slide) and find the Brewster angle.

-
Set up the components on the rail as shown on the
right. Turn the diode laser so that it shines on the middle of a glass slide in a holder on a
rotation stage.
The surface of the slide is vertical.
The angle of incidence can be changed by rotating the stage. Fix the rotation stage at 0.
Rotate the post in the holder until the light reflecting off the slide reflects
back onto itself in the horizontal direction, and then tighten the
post in the post holder. (Block the transmitted beam to
prevent it from shining into another person's face.)
- Rotate the polarizer in front of the screen by 90o,
so that its transmission axis is horizontal. It now blocks
vertically polarized light.
-
Using the rotation stage, rotate the slide approximately 55o.
Follow the reflected beam with the screen, by rotating the arm it is
mounted on. Find the angle at which the
reflected intensity is lowest.
- Iterate by adjusting the transmission axis of the polarizer and the
incident angle until the reflected intensity is practically zero.
Record the angle through which you have
rotated the rotation stage. This is the Brewster angle for the
glass slide in air.
- Use this measured value to find the
index of refraction of the microscope slide.
We have tanθB
= nglass/nair = nglass, since nair = 1.
- Is your value for nglass reasonable?
- Keep the rotation stage fixed at the Brewster angle and rotate
the polarizer. You should see a reflected beam. At the
Brewster angle the reflected beam should be 100% vertically
polarized.
- How do glare reducing sunglasses work?
Convert your log into a lab report.
See the grading scheme for all lab
reports.
Name:
E-mail address:
Laboratory 6 Report
- In one or two sentences, state the goal of this lab.
- Make sure you completed the entire lab and answered all parts. Make
sure you show your work and inserted and properly labeled relevant tables
and plots.
- Add a reflection at the end of your report in a short essay format.
Save your Word document (your name_lab6.docx), go to Canvas, Assignments, Lab
6, and submit your document.




 Turn on the light bulb by rotating the lens counterclockwise and removing it
completely.
Turn on the light bulb by rotating the lens counterclockwise and removing it
completely.


 Polarization by reflection
Polarization by reflection